6) The motion that creates energy

This rotation is what makes the energy “cumulate”; and consequently, speed increases a lot faster.

Let’s see the event in a drawing. I’ll draw the added quantity of energy as if coming from underneath the energy’s surface:

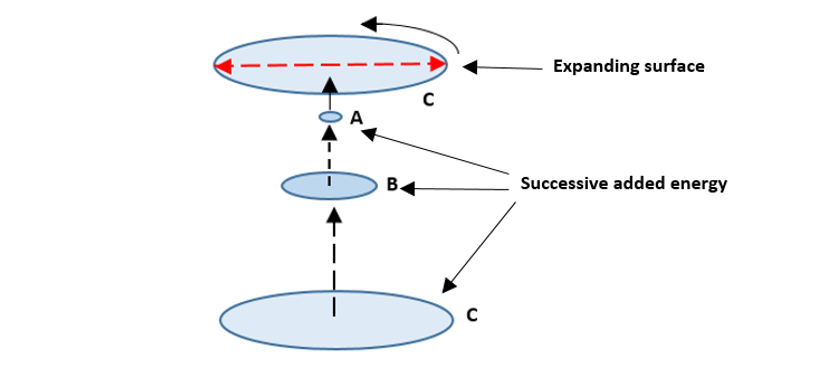
Let me explain the drawing.

A, B and C are moments in time; let’s say: 1st turn, 2nd turn and 3rd turn.

At “A”, there is only a bit of energy involved, and it makes a full rotation, increasing the tangential speed (kinetic energy) and the diameter.

So at “B” (start of second turn), all the kinetic energy present takes action, which doubles the amount of kinetic energy first involved.

The same event occurs at “C”, but then, it’s the previous doubled kinetic energy that doubles; so you have four times more energy involved than at the first rotation.

This constant adding of kinetic energy increases speed on top of the created rotating tangential speed (which is a second factor) that already doubles at every turn.

So if we put a value of “1” to the initial energy “point”, after the first completed rotation you get double speed = “2”, plus the double value of energy increase which totals 4 times the initial energy value. And then, this 4 times more energy value starts to operate.

At the end of the second rotation, you get an injection of the double speed of 4 = 8 times more than the initial energy, plus the value of 8 added tangential kinetic energy that, then, starts to operate; which is a total of 16 times more than the initial kinetic energy.

So in just two rotations, starting with a value of “1” you increased to a value of “16”.

There should be a formula to calculate this increasing “ratio”; but I don’t even want to think about it. I leave it to specialists.

The important fact is that we’ve found the operating process that increases the start of a zero point energy to its maximum.

And this increase of kinetic energy kept on going during all the Planck era, until it reached Planck time (10^-43 second after time = zero).

The next question that comes to mind is:

Why did it stop at Plank’s time (10^-43 sec)?